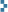
Operadores lineales, primer lema de Schur y mecánica cuántica

Y de repente, BatchDrake.

Hace mucho que no actualizo este blog, mi vida ha dado muchas vueltas desde mi último post y no puedo dedicarle a esto el tiempo que le dedicaba antes. Pero resulta que últimamente ando metido en un fregao que me obliga a aprender cosillas sobre mecánica cuántica, y estoy teniendo una serie de revelaciones de índole matemático que me gustaría compartir. De todos modos, no esperéis rigor en esta entrada, sólo intuiciones.

Como dijo cierto ponente en una conferencia sobre álgebras de Lie, años ha, en la Facultad de Matemáticas de Santiago de Compostela: «¡no desgeometricéis las matemáticas!», y aquí estoy yo, para geometrizar un poquito las cosas. No me gustan las cosas demasiado abstractas pero, desgraciadamente, este tema es abstracto de por sí, y aunque quiero acercar un poco esta matemática a los legos en la materia, es importante saber:

• Qué es un espacio vectorial. Y sobre todo, que existen espacios vectoriales cuyos vectores son funciones.
• Qué es una base vectorial.
• Qué es una base vectorial ortonormal.
• Qué es un un producto interior o escalar.

Los números cuánticos m y l determinan la «forma» de los orbitales de un átomo. Estos números cuánticos se corresponden con los valores posibles que puede tomar ciertos observables. Imagen tomada de Wikipedia.

¿Listo? Bueno, entonces la cosilla va tal que así: se ve que en la mecánica cuántica intervienen unos espacios vectoriales muy chulos, y cada vector de ese espacio vectorial representa un estado físico de tu sistema cuántico (como por ejemplo, el conocido ejemplo de la partícula en un campo de potencial central). Este espacio vectorial lo genera una base cuyos vectores representan una configuración determinada de magnitudes que estás teniendo en cuenta en tu sistema físico. Por ejemplo, si te interesan magnitudes como el momento angular orbital de un electrón (número cuántico l, esto se da en el bachillerato) y su proyección en el eje Z (número cuántico m), esa base podría estar formada por vectores como x := «estado del electrón tal que l = 3 y m = -2″ o y :=»estado del electrón tal que l = 1, m = 1″. Como son vectores, si yo sumo varios de estos vectores de la base (en general, si hago una combinación lineal con ellos) tendré otro vector: por ejemplo, si v = √2x +√2y, el vector v representa un estado donde el electrón tiene al mismo tiempo l=3,m=-2 y l=1,m=1 con la misma probabilidad. Sí, esto es posible, se llama superposición cuántica y tiene que ver con lo del gato de Schrödinger.

Si esta base es ortonormal, hacer la operación inversa (a partir de mi estado superpuesto, saber qué estados básicos lo forman) es trivial: haciendo el producto escalar de v por cada vector de la base (es decir, proyectando el estado sobre ese vector de la base), recupero los coeficientes que multiplican al vector básico correspondiente:

⟨x,v⟩ = ⟨x,√2x +√2y⟩ = √2⟨x,x⟩, +√2⟨x,y⟩ = √2 · 1 + √2 · 0 = √2

⟨y,v⟩ = ⟨y,√2x +√2y⟩ = √2⟨y,x⟩, +√2⟨y,y⟩ = √2 · 0 + √2 · 1 = √2

Pero claro, debo recalcar de nuevo con lo de podría estar formada, porque esta elección de la base no es obligatoria. Para un espacio vectorial de dimensión mayor que 1 (en este caso, dimensión infinita numerable, he jugado con los vectores x e y, pero en esa base habrá muchos más y me quedaría sin letras) hay infinitas bases que lo generan, y quizá v esté expresado como v = a · cosa0 + b · cosa1 + c · cosa2, siendo los vectores cosai alguna base rara, por lo que tendría que hacer un cambio de base y expresar cada uno de estos vectores como combinación de x, y y todos los demás. Esto es un lío, pero por suerte el formalismo matemático de la mecánica cuántica sistematiza estos casos de forma bastante satisfactoria. El truco está en usar operadores lineales hermíticos.

Operadores lineales (y operadores lineales hermíticos)

Aquí empieza la chicha, porque la matemática de la mecánica cuántica juega mucho con este concepto para hacer descripciones precisas de los estados de cada sistema. En esencia, un operador lineal es cierta transformación (lineal) sobre los vectores de un espacio vectorial en otro. El espacio de entrada y de salida no tiene por qué ser distinto, en el caso de la mecánica cuántica ambos espacios son iguales (la cosa se nos simplifica) y los operadores lineales hacen transformaciones de un vector de estado en otro vector de estado. ¿Para qué? Lo veremos ahora, pero antes, más intuiciones sobre operadores lineales:

Como dije antes, esto es una transformación lineal entre espacios vectoriales. Esta «transformación» se puede entender intuitivamente de la siguiente manera: dada una base ortonormal cualquiera (en general, ê₁, ê₂, ê₃, …, ên) si llamas a tu operador T y le pasas un vector v, el operador le hará lo siguiente:

Para cada elemento ê_i de la base:

1. Calculará el producto escalar de v por cierto vector ti: ⟨ti,v⟩
2. Tomará ese producto escalar y lo multiplicará por ê_i: ⟨ti,v⟩ê_i
3. Lo sumará a la salida y pasará al siguiente

Es decir, que el operador T(v) convierte v en ⟨t1,v⟩ê₁ + ⟨t2,v⟩ê₂ + ⟨t3,v⟩ê₃ + ⟨t4,v⟩ê₄ + … es decir, un operador lineal se define básicamente por tantos vectores ti como tena nuestra base vectorial. Es el vector mediante el cual se calculará el coeficiente de la base dada.

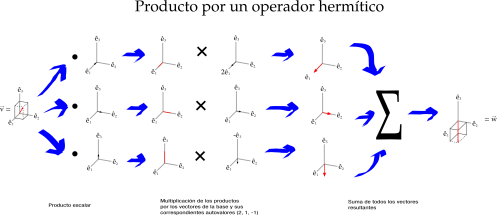
Un caso especialmente simple es cuando los vectores t_i coinciden con los ê_i de la base ortonormal (importante lo de ortonormal). En ese caso, el operador se define como:

I(v) = ⟨ê₁,v⟩ê₁ + ⟨ê₂,v⟩ê₂ + ⟨ê₃,v⟩ê₃ + ⟨ê₄,v⟩ê₄ + …

de modo que el vector v se proyecta en cada vector de la base… para volver a usarse como coeficiente de ese mismo vector de la base. La operación «descompone» y «recompone» el vector de entrada otra vez: lo deja como está. Esto es, ni más ni menos, el operador identidad.

Actuación del operador identidad sobre un vector cualquiera en el espacio euclídeo tridimensional.

Démosle unas vueltas más a esto. Si tu vector es v es 5ê₁ + 3ê₂ – ê₅ + 2ê₉ (por ejemplo), está claro que I(v) también será 5ê₁ + 3ê₂ – ê₅ + 2ê₉. Vamos a modificar este operador añadiéndole ciertos factores constantes ki a cada vector de la base y lo llamaremos L(v):

L(v) = k₁⟨ê₁,v⟩ê₁ +k₂⟨ê₂,v⟩ê₂ +k₃⟨ê₃,v⟩ê₃ + k₄⟨ê₄,v⟩ê₄ + …

Entonces, ¿qué le hará L al vector v?

L(5ê₁ + 3ê₂ – ê₅ + 2ê₉) =5k₁ê₁ + 3k₂ê₂ – k₅ê₅ + 2k₉2ê₉

Es decir, multiplica cada coeficiente del vector por un factor ki. Cuando un operador se define así, es dice que es un operador hermítico o autoadjunto. Los vectores de la base ortonormal ê₁, ê₂, ê₃ se llaman autovectores del operador (ya que no cambian de dirección, sólo en módulo y sentido: si entra un ê_i sale un ê_i multiplicado por algo). Los factores ki se llaman autovalores del operador.

Actuación de un operador hermítico sobre un vector cualquiera en el espacio euclídeo tridimensional. Este operador tiene los autovalores (2, 1, -1)

Bueno, todo esto está muy bien, ¿pero qué tiene que ver esto con la mecánica cuántica? Pues que nos arregla el problema de la elección de la base. Si forzamos a que esta base de vectores ê_i coincida con la base de vectores x, y, z… que hemos visto antes, tenemos un operador que ante un vector «estado puro» devuelve ese vector de estado puro multiplicado por un autovalor ki. Si este autovalor ki hacemos que coincida con el valor de alguna magnitud física asociada a ese «estado puro», tenemos un un operador asociado a un observable.

Por ejemplo, si nuestro J lo definimos de modo que la base sea x, y, z… y los autovalores sean por ejemplo el valor del número cuántico m, tenemos que L(x) = -2x, L(y) = y, y L(v) = L(√2x +√2y) = -2√2x +√2y. En este caso, L se corresponde con el observable «proyección del momento angular orbital en el eje Z«. Si v fuese un estado puro (que no lo es), L(v) sería múltiplo de v. Esto sería verdad para cualquier base (aunque L tenga internamente la suya propia).

Un par de anotaciones más: para cualquier operador asociado a un observable T, sus autovalores deben ser números reales.  Al fin y al cabo, las magnitudes físicas se miden también en números reales. Esto es una imposición de tipo físico, no matemático.

Además, cuando se hace una medida del observable correspondiente a T, el estado «colapsa» en alguno de los autovectores de T con una probabilidad que depende de los coeficienes de la superposición de estados. Por tanto, el valor de ese observable tras la medida es el ki del autovector. Esto es, de nuevo, un resultado físico.

Más sobre bases y el lema de Schur

Supongamos ahora dos operadores hermíticos T, U asociados a otros dos observables distintos cualesquiera. Aquí pueden suceder tres cosas:

a) El operador T y U tienen la misma base de autovectores. Esto quiere decir que puedo aplicar T sobre el estado y luego U, es lo mismo que aplicar U y luego T:

T(U(v)) = T(U(5ê₁ + 3ê₂ – ê₅ + 2ê₉)) = T(5u₁ê₁ + 3u₂ê₂ – u₅ê₅ + 2u₉ê₉) = 5t₁u₁ê₁ + 3t₂u₂ê₂ – t₅u₅ê₅ + 2t₉u₉ê₉

U(T(v)) = U(T(5ê₁ + 3ê₂ – ê₅ + 2ê₉)) = U(5t₁ê₁ + 3t₂ê₂ – t₅ê₅ + 2t₉ê₉) = 5t₁u₁ê₁ + 3t₂u₂ê₂ – t₅u₅ê₅ + 2t₉u₉ê₉

Cuando sucede esto, decimos que los operadores conmutan, porque entre ellos la propiedad conmutativa es cierta (esto para operadores lineales en general no es verdad). Como los autovectores no cambian de dirección, sólo de módulo y sentido, no importa el orden en el que U y T sean aplicados. El sentido físico de esto es que ambos observables pueden ser medidos con precisión arbitraria.

b) El operador T y U tienen distinta base de autovectores. En este caso, un autovector de T puede no serlo de U: Un autovector de T mantendrá su dirección tras ser aplicado a T, pero entonces U le cambiará la dirección. Y al revés, más de lo mismo, un autovector de U mantendrá su dirección, pero entonces T lo cambiará de dirección por ser «otra cosa». Cuando esto sucede, la precisión de la medida de un observable afecta irremediablemente a la precisión de la medida de otro: lo que es un «estado puro» de T, es una mezcla rara de estados para U. Y al revés, lo que es un estado puro de U, es una mezcla rara de estados para T. Cuando esto sucede, se dice que T y U no conmutan puesto que T(U(v)) no es el mismo operador que U(T(v)).

Esto no es, ni más ni menos, que el principio de incertidumbre de Heisemberg, pero con matemáticas (más o menos). Existen pares de magnitudes que no se pueden medir simultáneamente con total precisión, y esto no es una limitación tecnológica nuestra. Es que, a este nivel, ambas magnitudes dependen la una de la otra.

c) Cierto operador A conmuta con todos los operadores definidos en el espacio vectorial. Cuando eso pasa, quiere decir que cualquier vector que pase por este operador nunca va a cambiar de dirección. La única transformación será ser multiplicado por su autovalor. Pero claro, para que esta transformación nunca cambie la dirección de ningún vector, todos los autovalores deben ser los mismos (o tendríamos algo como que v = x + y podría ser transformado en 3x + 2y que ciertamente no tiene la dirección de v).

Lo único que hace este operador es multiplicar cada vector por el autovalor k.

Por lo tanto, A se comporta como escalar: su único autovalor (también se puede escribir como que A(v) = kI(v)). Esto se conoce como el primer lema de Schur, y es de vital importancia en cálculos de teoría de grupos, pues cuando este tipo de operador existe las operaciones se simplifican que da gusto.

Y hasta aquí. No me ha quedado un artículo muy divulgativo, lo admito. Pero sé que hay gente por ahí que, teniendo una base de álgebra primero de carrera, alguna vez se ha preguntado «de qué va esto» sin querer entrar en detalles. En parte, este artículo me lo estoy dedicando a mí mismo al empezar segundo de carrera. Pero en fin, la causalidad del universo en el que vivo me impide hacer ciertas cosas.

Saludos